10 Function factories

Published

July 22, 2025

Modified

July 24, 2025

Introduction

function factories就是能创建函数的函数。下面是一个示例：使用power1()函数生成square()和cube()函数。

power1 <- function(exp) {
  function(x) {
    x^exp
  }
}

square <- power1(2)
cube <- power1(3)

square()和cube()函数被称为manufactured functions，与function factories相对，这种叫称呼的唯一意义就是区分函数的来源，本质都是函数，没有区别。

square(3)
#> [1] 9
cube(3)
#> [1] 27

我们在之前章节中分别介绍了能够实现function factories的三大基石：

  • 6.2.3节，介绍了R中的函数都是第一类函数（first-class functions），使用<-直接将function()创建的函数赋值给变量。

  • 7.4.2节，介绍了在创建函数时会绑定创建时的环境，形成闭包。

  • 7.4.4节，介绍了函数每次运行时都会创建临时运行环境——最终变成manufunction factories的闭包环境。

本章，我们介绍如何使用上述的三个概念，创建function factories，并将其应用到可视化与统计处理中。

在三种主要的泛函编程工具(functionals, function factories, and function operators)中，function factories是使用最少的。总的来说，它们并不倾向于降低整体代码复杂度，而是将复杂度分割成更容易理解的块。函数工厂也是非常有用的函数运算符的重要组成部分，你将在第 11 章中学习。

Outline

  • 10.2节：function factories如何工作和使用
  • 10.3节：在可视化中的应用
  • 10.4节：在统计分析中的应用
  • 10.5节：与泛函联用

Prerequisites

熟悉6.2.3，7.4.2，7.4.4章节中的内容。

我们使用rlang包检视function factories；使用ggplot2，scale包创建可视化示例。

library(rlang)
library(ggplot2)
library(scales)

Factory fundamental

实现function factories的关键原理可以表述为：function factories的执行环境是manufactured functions的创建（闭包）环境。本节将通过互动探索和一些图表帮助你更深刻地理解这一原理。

Environments

首先查看一下square()和cube()函数。

square
#> function (x) 
#> {
#>     x^exp
#> }
#> <environment: 0x000002bf1dd66e08>

cube
#> function (x) 
#> {
#>     x^exp
#> }
#> <bytecode: 0x000002bf1deac278>
#> <environment: 0x000002bf1dd86ac8>

从两个函数的结构中，我们可以清晰地知道参数x的值来源，但参数exp的值来源呢？仔细观察会发现，两个函数的主体结构是相同的，它们绑定的创建环境不同。

下面我们使用rlang::env_print()函数查看各自的创建环境。

env_print(square)
#> <environment: 0x000002bf1dd66e08>
#> Parent: <environment: global>
#> Bindings:
#> • exp: <dbl>

env_print(cube)
#> <environment: 0x000002bf1dd86ac8>
#> Parent: <environment: global>
#> Bindings:
#> • exp: <dbl>

从结果中，我们可以看到两个函数的创建函数的父环境都是全局环境，同时都绑定了变量exp。

我们使用rlang::fn_env()函数查看环境中变量的值。

fn_env(square)$exp
#> [1] 2

fn_env(cube)$exp
#> [1] 3

终于，我们找到了square和cube函数的不同之处：square函数的创建环境绑定的变量exp的值为2，而cube函数的创建环境绑定的变量exp的值为3。

Diagram conventions

power1()，square()，cube()三个函数的关系可以用下面示意图表示：

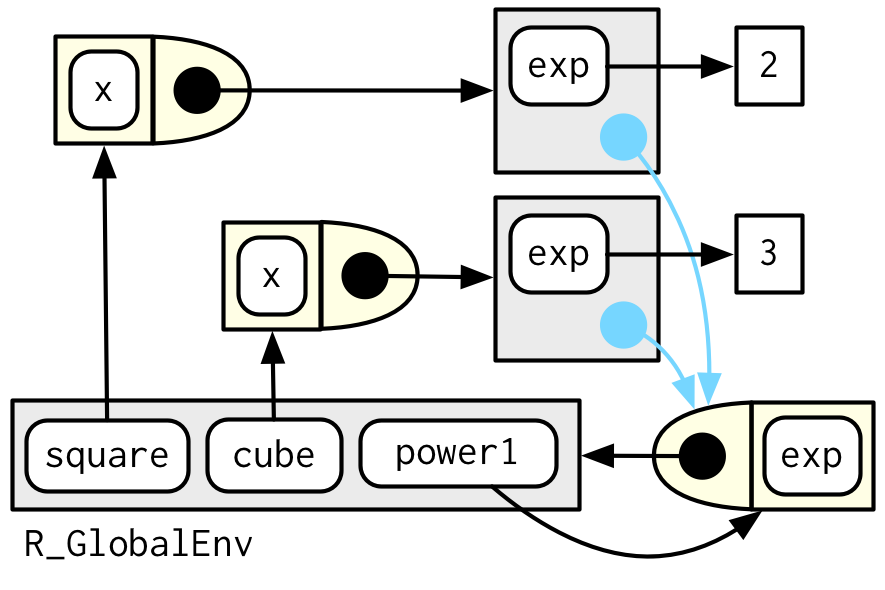
不考虑过多细节，我们可以抽象出下面两条规律：

  • 任何自由浮动的变量都存在于全局变量（function factories的创建环境）中。

  • 任何没有显式父级的环境都继承自全局环境（function factories的创建环境）。

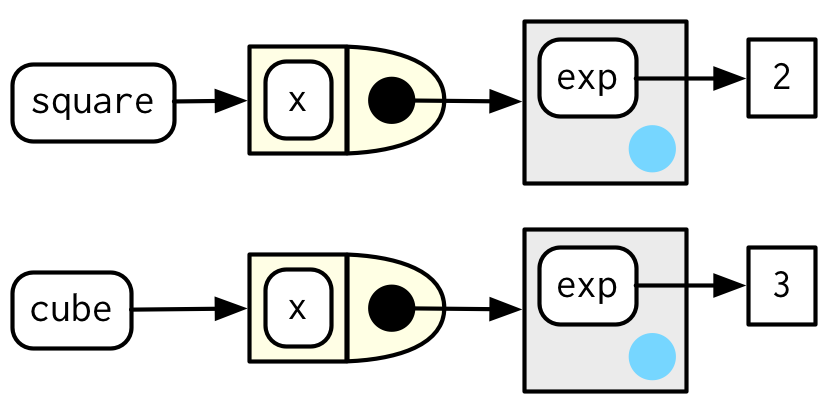
当执行square(10)时，我们可以预料到：x^exp中的x在函数的执行环境中，exp在函数的创建环境中。

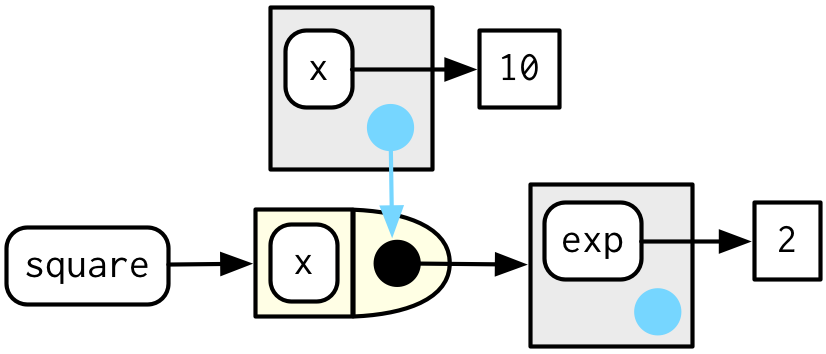
Forcing evaluation

在实际使用过程中，power1()函数会因为延迟评估造成bug。

x <- 2
square <- power1(x)
x <- 3

此时运行square(2)，不会返回4，而是8。

square(2)
#> [1] 8

因为power1()中的x只有在square()被调用时才会被评估。这种由于延迟评估造成的bug，在由function factories生成manufactured functions时广泛存在。

我们可以使用force()函数来强制在创建square()时，power1()的参数x就被评估。

power2 <- function(exp) {
  force(exp)
  function(x) {
    x^exp
  }
}

x <- 2
square <- power2(x)
x <- 3
square(2)
#> [1] 4

如果输入的参数被调用，那么它就可以被视作“force”了。例如exp <- exp + 1 - 1。

power3 <- function(exp) {
  exp <- exp + 1 - 1
  function(x) {
    x^exp
  }
}
x <- 2
square <- power3(x)
x <- 3
square(2)
#> [1] 4

Stateful functions

6.4.3节中讲到，函数每次执行都会创建执行环境，我们无法将函数的第一次调用与第二次调用进行关联。但是function factories可以允许我们进行关联，保持每次调用时的状态。

  • manufactured functions的执行环境是function factories的创建环境——唯一且固定。

  • R 中的<<-允许修改创建环境中的变量。

下面是一个记录函数被调用次数的状态函数例子：

new_counter <- function() {
  i <- 0

  function() {
    i <<- i + 1
    i
  }
}

counter_one <- new_counter()
counter_two <- new_counter()

counter_one()和counter_two()创建时，i的初始值是0。

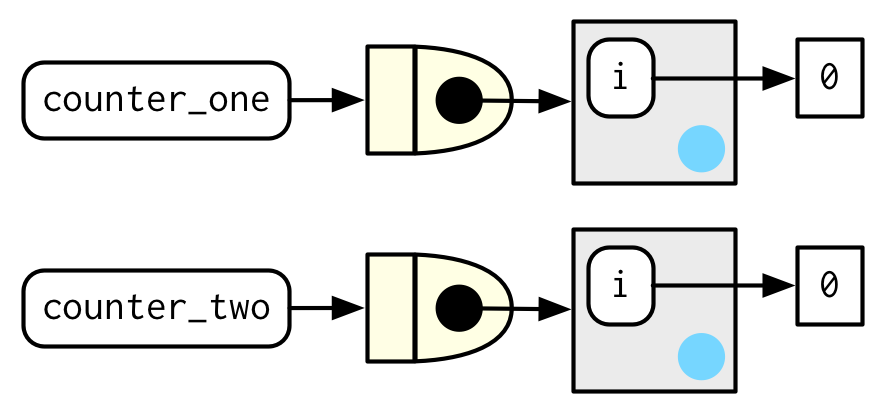
每被调用一次，i的值都会加1。

counter_one()
#> [1] 1
counter_one()
#> [1] 2
counter_two()
#> [1] 1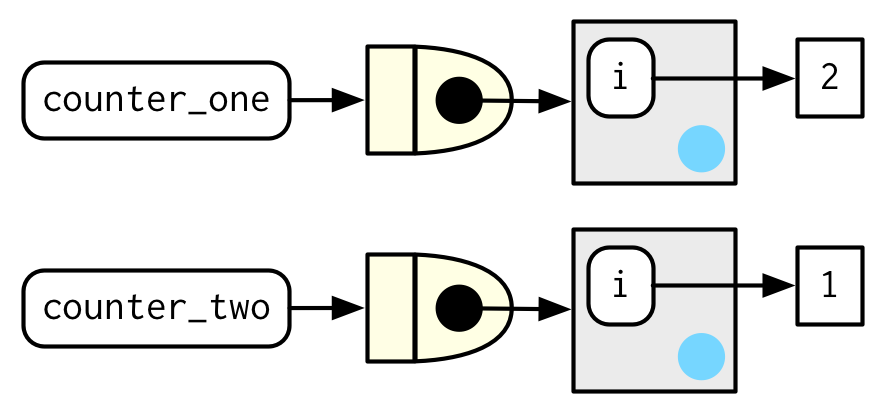

状态函数最好用于调节。一旦函数开始管理多个变量的状态，最好切换到 R6 面向对象, 我们会在第14章中介绍。

Garbage collection

因为manufactured functions的执行环境是唯一且固定的，我们无法在全局环境中删除其创建的变量，当它内部创建了内存消耗过大的变量时，我们要手动定义删除这些变量。

f1 <- function(n) {
  x <- runif(n)
  m <- mean(x)
  function() m
}

g1 <- f1(1e6)
lobstr::obj_size(g1)
#> 8.00 MB

f2 <- function(n) {
  x <- runif(n)
  m <- mean(x)
  rm(x)
  function() m
}

g2 <- f2(1e6)
lobstr::obj_size(g2)
#> 504 B

Graphical factories

本节我们给出一些应用function factories到ggplot2的例子。

Labelling

scales 包提供了许多function factories，例如其中的formatter函数：它根据参数返回一个函数，用来生成不同格式的标签。

y <- c(12345, 123456, 1234567)
comma_format()(y)
#> [1] "12,345"    "123,456"   "1,234,567"

number_format(scale = 1e-3, suffix = " K")(y)
#> [1] "12 K"    "123 K"   "1 235 K"

scales 包的这些function factories，可以说就是为了ggplot2服务的，例如laebls参数需要提供的值就是一个函数，用来对轴标签进行格式化。

df <- data.frame(x = 1, y = y)
core <- ggplot(df, aes(x, y)) +
  geom_point() +
  scale_x_continuous(breaks = 1, labels = NULL) +
  labs(x = NULL, y = NULL)

core

core + scale_y_continuous(
  labels = comma_format()
)

core + scale_y_continuous(
  labels = number_format(scale = 1e-3, suffix = " K")
)

core + scale_y_continuous(
  labels = scientific_format()
)

Histogram bins

geom_histogram()的binwidth参数除接受一个数值外，也可以接受一个函数。函数在分组绘制histogram时十分有用，因为它会按组别计算bin宽度，保持bin的数目一致。下面是一个例子：

# construct some sample data with very different numbers in each cell
sd <- c(1, 5, 15)
n <- 100

df <- data.frame(x = rnorm(3 * n, sd = sd), sd = rep(sd, n))

ggplot(df, aes(x)) +
  geom_histogram(binwidth = 2) +
  facet_wrap(~sd, scales = "free_x") +
  labs(x = NULL)

我们在生成数据时，每个组的数据量是相同的，但区间不同；导致当设置binwidth参数为固定值时，不同组别的bin数目不同的，相反我们应该固定bin的数目，根据bin数据计算binwidth。

binwidth_bins <- function(n) {
  force(n)

  function(x) {
    (max(x) - min(x)) / n
  }
}

ggplot(df, aes(x)) +
  geom_histogram(binwidth = binwidth_bins(20)) +
  facet_wrap(~sd, scales = "free_x") +
  labs(x = NULL)

base R 提供了一些计算最优binwidth的函数，例如nclass.Sturges(),nclass.scott(),nclass.FD()，我们可以将其打包成一个function factories。

base_bins <- function(type) {
  fun <- switch(type,
    Sturges = nclass.Sturges,
    scott = nclass.scott,
    FD = nclass.FD,
    stop("Unknown type", call. = FALSE)
  )

  function(x) {
    (max(x) - min(x)) / fun(x)
  }
}

ggplot(df, aes(x)) +
  geom_histogram(binwidth = base_bins("FD")) +
  facet_wrap(~sd, scales = "free_x") +
  labs(x = NULL)

ggsave()

gglot2 中的ggsave()函数，其内部使用了一个function factories——plot_dev()。 其根据文件后缀判断图片类型，选择合适的绘图设备。下面是plot_dev()的简化示例：

plot_dev <- function(ext, dpi = 96) {
  force(dpi)

  switch(ext,
    eps = ,
    ps = function(path, ...) {
      grDevices::postscript(
        file = filename, ..., onefile = FALSE,
        horizontal = FALSE, paper = "special"
      )
    },
    pdf = function(filename, ...) grDevices::pdf(file = filename, ...),
    svg = function(filename, ...) svglite::svglite(file = filename, ...),
    emf = ,
    wmf = function(...) grDevices::win.metafile(...),
    png = function(...) grDevices::png(..., res = dpi, units = "in"),
    jpg = ,
    jpeg = function(...) grDevices::jpeg(..., res = dpi, units = "in"),
    bmp = function(...) grDevices::bmp(..., res = dpi, units = "in"),
    tiff = function(...) grDevices::tiff(..., res = dpi, units = "in"),
    stop("Unknown graphics extension: ", ext, call. = FALSE)
  )
}

plot_dev("pdf")
#> function (filename, ...) 
#> grDevices::pdf(file = filename, ...)
#> <bytecode: 0x000002bf26845b70>
#> <environment: 0x000002bf264bcd30>
plot_dev("png")
#> function (...) 
#> grDevices::png(..., res = dpi, units = "in")
#> <bytecode: 0x000002bf1f72e618>
#> <environment: 0x000002bf1f30c928>

Statistical factories

本节介绍一些统计分析中运用到的function factories例子。

Box-Cox transformation

Box-Cox变换是一种常用的数据变换方法，用于处理非正态数据正态化。唯一参数是λ，用来控制转换强度。Box-Cox变换可以用下面的函数实现：

boxcox1 <- function(x, lambda) {
  stopifnot(length(lambda) == 1)

  if (lambda == 0) {
    log(x)
  } else {
    (x^lambda - 1) / lambda
  }
}

我们将上面的函数转换为一个function factories，用其探索不同λ对数据的影响。

boxcox2 <- function(lambda) {
  if (lambda == 0) {
    function(x) log(x)
  } else {
    function(x) (x^lambda - 1) / lambda
  }
}

stat_boxcox <- function(lambda) {
  stat_function(aes(color = lambda), fun = boxcox2(lambda), linewidth = 1)
}

ggplot(data.frame(x = c(0, 5)), aes(x)) +
  lapply(c(0.5, 1, 1.5), stat_boxcox) +
  scale_colour_viridis_c(limits = c(0, 1.5))

ggplot(data.frame(x = c(0.01, 1)), aes(x)) +
  lapply(c(0.5, 0.25, 0.1, 0), stat_boxcox) +
  scale_colour_viridis_c(limits = c(0, 1.5))

Bootstrap generators

在统计分析工作中，我们经常需要多个Bootstrap生成器，这个时候构建一个Bootsrap生成器的function factories就显得很有必要。

下面是一个对数据框中某列进行随机抽样的例子：

boot_sample <- function(df, var) {
  n <- nrow(df)
  force(var)

  function() {
    col <- df[[var]]
    col[sample(n, replace = TRUE)]
  }
}

boot_mtcars1 <- boot_sample(mtcars, "mpg")
head(boot_mtcars1())
#> [1] 33.9 18.1 33.9 24.4 13.3 26.0
head(boot_mtcars1())
#> [1] 22.8 15.2 33.9 21.4 17.8 10.4

有时我们需要构建一个根据模型生成随机样本的Bootstrap生成器。

boot_model <- function(df, formula) {
  model <- lm(formula, data = df)
  fitted <- unname(fitted(model))
  resid <- unname(resid(model))
  rm(model)

  function() {
    fitted + sample(resid)
  }
}

boot_mtcars2 <- boot_model(mtcars, mpg ~ wt + disp)
head(boot_mtcars2())
#> [1] 29.69387 22.45676 22.68264 17.29761 14.38976 18.10000
head(boot_mtcars2())
#> [1] 25.54030 20.17392 25.23816 19.83821 18.45017 18.10000

Maximum likelihood estimation

最大似然估计（MLE）用来找到某个分布的参数，使得观测数据在该分布下出现概率最大。下面我们使用泊松分布来演示如何通过function factories优雅的实现最大似然估计。

泊松分布的公式如下，当已知参数λ后，我们可以计算观察数据\(X\)的概率：

\[ P(\lambda,{\bf x})=\prod_{i=1}^{n}\frac{\lambda^{x_{i}}e^{-\lambda}}{x_{i}!} \]

在统计中，我们通常对数化累乘公式，将其转换为累加：

  • 累加的计算量小
  • 累乘在计算机中会导致浮点数精确度下降

\[ \log(P(\lambda,{\bf x})) = \sum_{i=1}^{n}\log\left(\frac{\lambda^{x_i}e^{-\lambda}}{x_i!}\right) \]

\[ \log(P(\lambda,{\bf x})) = \sum_{i=1}^{n}\left(x_i\log(\lambda) - \lambda - \log(x_i!)\right) \]

\[ \log(P(\lambda,{\bf x})) = \sum_{i=1}^{n}x_i\log(\lambda) - \sum_{i=1}^{n}\lambda - \sum_{i=1}^{n}\log(x_i!) \]

\[ \log(P(\lambda,{\bf x})) = \log(\lambda)\sum_{i=1}^{n}x_i - n\lambda - \sum_{i=1}^{n}\log(x_i!) \]

构造已知λ后计算观察数据\(X\)概率的函数：

mle_poisson <- function(lambda, x) {
  # x 相对是固定的，提前计算，可以节省计算资源
  sum_x <- sum(x)
  n <- length(x)
  c <- sum(lfactorial(x))
  # log(lambda) * sum(x) - n * lambda - sum(lfactorial(x))
  log(lambda) * sum_x - n * lambda - c
}

使用base R 计算观察数据\(X\)的概率：

x1 <- c(41, 30, 31, 38, 29, 24, 30, 29, 31, 38)
mle_poisson(10, x1)
#> [1] -183.6405
mle_poisson(20, x1)
#> [1] -61.14028
mle_poisson(30, x1)
#> [1] -30.98598

虽然我们可以计算已知λ下的观察数据\(X\)的概率，但是最大似然估计要求我们找到一个λ，使得该概率最大。我们可以构造一个观察数据\(X\)的function factories，并使用optimize()函数来寻找最大概率的λ。

mle_poisson2 <- function(x) {
  force(x)
  function(lambda) {
    mle_poisson(lambda, x)
  }
}

optimise(mle_poisson2(x1), interval = c(0, 100), maximum = TRUE)
#> $maximum
#> [1] 32.09999
#> 
#> $objective
#> [1] -30.26755

借助optimize()函数的...参数，我们可以直接使用下面的代码：

optimise(mle_poisson, interval = c(0, 100), x = x1, maximum = TRUE)
#> $maximum
#> [1] 32.09999
#> 
#> $objective
#> [1] -30.26755

Function factories + functionals

组合使用function factories和functionals，可以通过map系函数传递参数，构造出一个函数集合。如果你的function factories需要多个参数，就使用相应的map系函数。

names <- list(
  square = 2,
  cube = 3,
  root = 1 / 2,
  cuberoot = 1 / 3,
  reciprocal = -1
)
funs <- purrr::map(names, power1)

funs$root(64)
#> [1] 8
funs$root
#> function (x) 
#> {
#>     x^exp
#> }
#> <bytecode: 0x000002bf1deac278>
#> <environment: 0x000002bf24488780>

在上面的例子中，你需要使用funs$来提取函数，下面有三种方法可以直接使用funs内部的函数：

  • 使用with()，临时提取函数
with(funs, root(64))
#> [1] 8
  • 使用attach()，将函数绑定到当前环境
attach(funs)
#> The following objects are masked _by_ .GlobalEnv:
#> 
#>     cube, square
root(100)
#> [1] 10
detach(funs)
  • 使用rlang::env_bind()，将函数绑定到当前环境
rlang::env_bind(globalenv(), !!!funs)
root(100)
#> [1] 10
rlang::env_unbind(globalenv(), names(funs))
Back to top